Understanding Kirchhoff's Laws: Theory, Examples, and Applications

Electrical-World Admin
22 Oct 2024

Kirchhoff's Laws, despite their simplicity, are powerful tools that help analyze complex electrical circuits. They elegantly describe the current and voltage behavior throughout various branches of an electric circuit. In this paper, we delve into Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL), using examples from everyday life, formulas, and tables to illustrate just how significant and accessible these laws are.

What Are Kirchhoff's Laws?

Kirchhoff's Laws consist of two essential principles used in circuit analysis:

Kirchhoff's Current Law (KCL): The total current flowing into a junction is equal to the total current flowing out of it.
Kirchhoff's Voltage Law (KVL): The sum of all voltages of a closed loop in a circuit equals zero.

These formulas are based on the conservation of energy and charge, making them powerful tools for solving circuit problems involving multiple loops and junctions.

Kirchhoff's Current Law (KCL)

KCL states that for any electrical junction:

\sum I_{\text{in}} = \sum I_{\text{out}}

Where:

$I_{\text{in}}$ is the current flowing into the junction,
$I_{\text{out}}$ is the current flowing out.

This law is based on the principle that charge cannot accumulate at a node.

Kirchhoff's Voltage Law (KVL)

KVL states that for any closed loop in a circuit, the sum of the electromotive forces (EMF) and voltage drops must equal zero:

\sum V = 0

Where:

$V$ represents the voltage around the loop.

KVL is derived from energy conservation, ensuring that the total voltage gained in the loop equals the total voltage dropped.

Application of Kirchhoff's Laws in Circuit Analysis

Let's consider an example of how to apply both KCL and KVL in solving a circuit.

Example Circuit

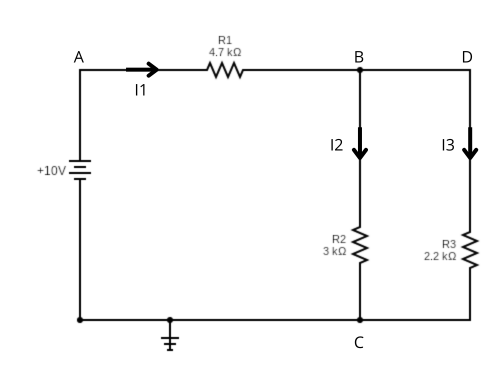
In this circuit, three resistors, $R_1$ , $R_2$ , and $R_3$ , are connected to a voltage source, $V$ . We will use KCL and KVL to find the current through each resistor.

Step 1: Applying KCL at Junction B

At junction B, currents $I_1$ , $I_2$ , and $I_3$ meet. According to KCL:

I_1 = I_2 + I_3

Step 2: Applying KVL in Loop A-B-C

Using KVL, we sum the voltages around the loop A-B-C:

V - I_1 R_1 - I_2 R_2 = 0

Step 3: Applying KVL in Loop B-D-C

For the second loop B-D-C:

I_2 R_2 - I_3 R_3 = 0

By solving these equations, we can determine the current through each resistor.

Kirchhoff's Laws in Real-World Applications Kirchhoff's Laws, with their practicality, are widely used in various fields such as:

Kirchhoff's Laws are widely used in various fields such as:

Power Distribution Systems: Ensuring electricity flows efficiently through different grid branches.
Electronic Circuit Design: Calculate the correct values of components to ensure devices operate as intended.
Signal Processing: Analyzing complex signal paths in communication networks.

Table: Comparison of Kirchhoff's Laws

Law	Statement	Example
Kirchhoff's Current Law	The Sum of currents entering a node equals the sum leaving it.	Used to analyze current flow in parallel circuits.
Kirchhoff's Voltage Law	The Sum of voltages around a loop is zero.	Used for solving voltage drops in series circuits.

Example: Power Grid

In a power grid, KCL ensures that the total power supplied by the generators equals the energy consumed by loads, accounting for power losses. KVL ensures the proper functioning of the transmission lines by maintaining the required voltage levels across long distances.

Kirchhoff's Laws: Mathematical Models

We can express the current-voltage relationships in a mathematical model to solve for unknowns in a circuit.

Consider Ohm's Law:

V = IR

By combining Kirchhoff's Voltage Law with Ohm's Law, we can solve for the currents in complex circuits.

For a system with $n$ loops and $m$ nodes, KCL and KVL provide a system of $n + m$ equations, which can be solved to determine all the unknown voltages and currents.

Formula: Power Dissipation in a Circuit

The power dissipated is calculated using the following formula:

P = I^2 R

Where:

$P$ is the power in watts (W),
$I$ is the current in amperes (A),
$R$ is the resistance in ohms (Ω).

Practical Considerations for Circuit Design

When designing circuits, engineers use Kirchhoff's Laws to:

Optimize component values for efficiency and safety.
Ensure energy conservation across the circuit.
Predict the behavior of the circuit under different load conditions.

Circuit Simulation Tools

Today, Kirchhoff's Laws are in various circuit simulation software, like SPICE, which allows engineers to simulate circuit performance before physical implementation.

Conclusion

Kirchhoff's Laws are foundational and indispensable in electrical engineering and circuit analysis. Understanding how current and voltage behave at junctions and around loops is the key to analyzing and designing even the most complex electrical systems. Whether you're working on small electronic circuits or large power grids, Kirchhoff's Laws provide the essential framework for ensuring functionality and efficiency.